
КЛАССИФИКАЦИЯ МЕТОДОВ БАЛАНСИРОВКИ
НАГРУЗКИ ПРОЦЕССОРОВ ПРИ РАСПРЕДЕЛЕННОМ
МОДЕЛИРОВАНИИ ЦИФРОВЫХ УСТРОЙСТВ
Бельков
Д
.
В
.
Кафедра
ВМиП
ДонНТУ
Abstract
Belkov D.V. The classification of load balancing methods for distributed
simulation of digital devices. This paper reviews the major load balancing
algorithms and discusses their relative merits on distributed simulation of
digital devices. The classification of load balancing methods is proposed.
Введение
В условиях ограниченности вычислительных ресурсов существенно
снизить затраты на моделирование цифровых устройств (ЦУ) за счет
параллельных вычислений позволяет использование компьютерных сетей.
Важной задачей распределенного моделирования ЦУ является разбиение
схемы на подсхемы и распределение подсхем на моделирующие
процессоры. Исходную схему можно представить в виде графа, в котором
вершины соответствуют элементам, а ребра – электрическим цепям
исходной схемы. В таком случае задача разбиения схемы на подсхемы
формулируется как задача разбиения графа на подграфы. Алгоритмы
разбиения графов должны обеспечивать балансировку нагрузки
процессоров и минимальное число межпроцессорных обменов [1].
Таким образом, при распределенном моделировании ЦУ на этапе
разбиения графа схемы на подграфы для повышения эффективности
моделирования необходимо решить задачу балансировки нагрузки
процессоров.
Применение статических методов балансировки нагрузки может
привести к блокировке процессов, заранее распределенных по
процессорам. Этого недостатка лишены динамические методы
балансировки, которые допускают миграцию процессов по процессорам в
зависимости от нагрузки.
Целью
данной
статьи
является
классификация
методов
динамической
балансировки,
которые
можно
применять
при
распределенном моделировании цифровых устройств.
Классификация
методов
балансировки
нагрузки
Простой моделью параллельных вычислений является модель
Master/Slave. Имеется главный (мастер) процессор и подчиненные (slave)
процессоры. Подчиненные процессоры выполняют вычисления и
обращаются к мастеру для дальнейшей обработки. Существует много
различных вариантов этой модели, например, может быть несколько типов
главных процессоров или иерархия подчиненных процессоров. Однако
подход Master/Slave целесообразно
использовать
только,
если
вычислительные задания выполняются независимо и асинхронно каждым
процессором. Количество сообщений между мастером и подчиненными
процессорами должно быть небольшим [2].
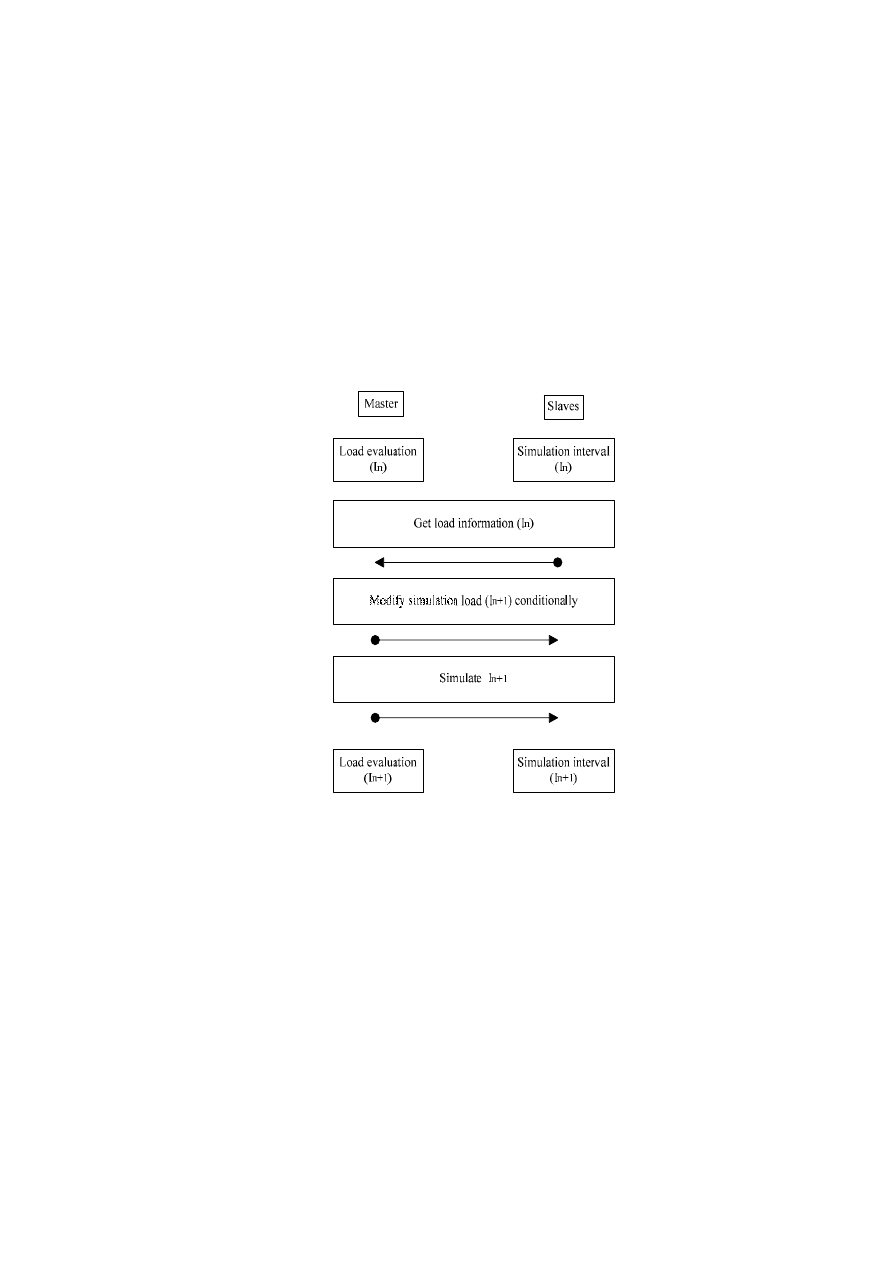
В работе [3] предложена система параллельного моделирования
цифровых устройств dlbSIM. Она содержит главный (master) компонент и
множество подчиненных (slave) компонент. Блок управления загрузкой
системы dlbSIM показан на рисунке 1.
Рисунок 1.- Блок управления загрузкой системы dlbSIM
Каждый подчиненный компонент запускается на отдельном
процессоре и выполняет процесс моделирования одной или нескольких
подсхем, состоящий из 4 шагов:
1.
CLOCK – выполнение моделирования всех подсхем, назначенных
на процессор, в течение заданного интервала моделирования.
2.
GET – Запись управляющих сигналов в выходные порты
процессора.
3.
TRANSFER – синхронизация работы подчиненных компонент.
4.
PUT – Чтение данных, необходимых для продолжения
моделирования из входных портов процессора.
Балансировка
загрузки
процессоров
выполняется
главным
компонентом на шаге TRANSFER. Целью является сокращение времени

моделирования всей схемы за счет выравнивания интервалов
моделирования подсхем на каждом процессоре.
Блок управления загрузкой, используя информацию о загрузке
процессоров, оценивает и модифицирует уровень их загрузки. В течение
интервала моделирования
(шаг CLOCK), подчиненные компоненты
работают независимо от главного компонента. После завершения
интервала
информация о загрузке процессоров передается главному
компоненту, который сравнивает ее с информацией о загрузке
процессоров на интервале
n
I
n
I
1
n
I
−
и принимает решение о необходимости
модификации загрузки. Для эффективной работы системы моделирование
подсхем должно происходить независимо и асинхронно на каждом из
подчиненных компонентов.
Другим примером модели Master/Slave является алгоритм
инициативного сервера [4]. Владеющий маркером узел (мастер), если его
нагрузка меньше пороговой величины, ищет наиболее нагруженный узел
сети и забирает у него такое количество запросов, которое необходимо для
достижения пороговой величины. Поиск наиболее нагруженного узла
выполняется путем посылки сообщений ко всем другим узлам и получения
от них соответствующих ответов о нагрузке. После завершения процесса
балансировки нагрузки маркер передается узлу с минимальной нагрузкой.
Геометрический подход разбиения графов требует, чтобы вершины
графа имели геометрические координаты. Это возможно не для всех
графов. Геометрические алгоритмы идеальны для параллельного
выполнения, но не учитывают структуру графа [2].
Алгоритм RCB (Recursive Coordinate Bisection) был впервые
предложен Бергером и Бохари как статический алгоритм. В нем
используются разрезающие плоскости, которые ортогональны одной из
координатных осей и выбирается плоскость, разрезающая наименьшее
число ребер графа. Алгоритм RCB разделяет граф на части без учета их
свойств. Этого недостатка нет у метода URB (Unbalanced Recursive
Coordinate Bisection), который разделяет граф на q частей при
соотношении их размеров: 1:(q-1) или 2:(q-2) и т.д. Простота и
быстродействие RCB и URB привлекательны для динамической
балансировки, однако недостатком этих алгоритмов является плохое
качество разбиения графа.
Алгоритм RIB (Recursive Inertial Bisection) использует понятия
механики. Целью является определение центра масс и направления
инерционного движения, вдоль которого вершины графа имеют
минимальный вращающий момент. Разрезающая плоскость выбирается
так, чтобы она была ортогональна к этому направлению [2].
Известен метод, который взамен разрезающей плоскости использует
сферу. Ее внутренняя часть соответствует одному разделу графа, а

внешняя часть – другому. Этот алгоритм является более сложным и
затратным, чем алгоритмы, использующие разрезающие плоскости, но
может быть легче распараллелен [2].
При использовании глобальных методов балансировки нагрузки
процессоры выполняют вычисления синхронно, а затем следует фаза
балансировки. При этом недогруженные процессоры вынуждены
простаивать, ожидая пока сильно загруженные процессоры, завершат
вычисления. Только после этого выполняется процесс балансировки.
Локальные
методы
балансировки
нагрузки
бывают
как
синхронными, так и асинхронными. Соседние процессоры могут
выполнять балансировку, в то время как другие процессоры заняты
вычислениями. Процессом балансировки можно управлять с помощью
запросов, поступающих от процессоров, когда они простаивают [4].
Многие локальные методы имеют 2 шага. На первом шаге
определяется, сколько работ будет перемещаться от одного процессора к
соседнему для балансировки нагрузки. На втором шаге используются
эвристики для выбора объектов, которые будут мигрировать. Эти
эвристики минимизируют коммуникационные затраты. Большинство работ
основано на алгоритме Кернигана-Лина (KL) или алгоритме KL/FM [1].
При определении потока работ может быть использован алгоритм
Кубенко [2]. Считается, что рабочая нагрузка удовлетворяет уравнению
u
t
/
u
2
∇
α
=
∂
∂
, где u - рабочая нагрузка,
α
- коэффициент диффузии. Для
решения уравнения применяется метод конечных разностей. Рабочая
нагрузка
на
итерации (t+1) вычисляется
по
формуле
, где
- рабочая нагрузка на итерации t, j –
номер процессора. Если i- й и j- й процессоры не соединены, то
∑
−
α
+
=
+
j
t
i
t
j
ij
t
i
1
t
i
)
u
u
(
u
u
t
i
u
0
ij
=
α
,
иначе
и
0
ij
>
α
∑
≥
α
−
j
ij
0
1
.
Метод Ху и Блейка [2] минимизирует поток работ через ребра графа
процессоров методом сопряженных градиентов. Решается система
уравнений
, где
- разность между загрузкой процессора i и
средней загрузкой процессоров. Элементы вектора X должны принимать
значения 1 или -1:
, если вершина i должна быть в первом подграфе
и
если вершина i должна быть во втором подграфе,
B
LX
=
i
B
1
X
i
=
1
X
i
−
=
∑
=
i
i
0
X
.
Значение
равно весу вершины i, если i=j. Если
ij
L
j
i
≠
и вершины i и j
соединены, то
1
L
ij
−
=
. Если
j
i
≠ и вершины i и j не соединены, то
0
L
ij
= .
Кроме геометрического подхода при разбиении графов применяется
структурный подход. Структурные методы можно разделить на методы
обхода графа и спектральные методы.

Алгоритм рекурсивной структурно-уровневой бисекции [5]
определяет максимально близкие вершины, вычисляя расстояние между
ними. Затем от этих вершин выполняется поиск в ширину. Половина
вершин графа помещается в первый подграф, вторая половина – во второй
подграф. Алгоритм повторяется для каждого подграфа. Этот алгоритм
обладает высоким быстродействием, но получаемое разбиение имеет
плохое качество. Поиск в ширину применяется также жадным
алгоритмом Фархата [5], но подграфы конструируются, начиная с
вершины, выбранной произвольно. Вес каждого подграфа равен
p
/
|
V
|
,
где |V| - число вершин графа, p – число процессоров. Похожим алгоритмом
является жадный алгоритм растущего графа, предложенный Кариписом и
Кумаром. Он конструирует подграфы для бисекции, начиная с
произвольного корня. Вершины добавляются в подграф в таком порядке,
чтобы минимизировалось число обрезанных ребер [5].
Спектральный метод RSB решает задачу, которую можно
сформулировать следующим образом. Необходимо найти вектор X, где
, если вершина i должна быть в первом подграфе и
если
вершина i должна быть во втором подграфе,
1
X
i
=
1
X
i
−
=
∑
=
i
i
0
X
,
, где
значение
равно весу вершины i, если i=j. Если
j
min
LX
X
T
→
ij
L
i
≠ и вершины i и j
соединены, то
1
L
ij
−
=
. Если
j
i
≠ и вершины i и j не соединены, то
0
L
ij
= .
Алгоритм RSB использует собственный вектор матрицы,
ассоциированный с вершинами графа. Хотя этот метод имеет высокое
качество результата, определение собственного вектора матрицы требует
значительных вычислительных затрат.
Для повышения качества разбиения графа могут быть использованы
уточняющие методы, например, алгоритм KL/FM или имитации отжига
[2].
В работе [6] приведен итеративный динамический метод разбиения
графов
с
учетом
балансировки
нагрузки
при
минимизации
межпроцессорных связей. Алгоритм KL используется совместно с
алгоритмом Ху и Блейка. Предложенный метод применяется системой
JOSTLE.
В многоуровневых методах балансировки оригинальный граф
подвергается серии преобразований, которые сводят его к более простому
графу. Полученный после преобразования граф, разбивается на подграфы с
помощью одного из известных алгоритмов, разбиение этого графа может
быть выполнено быстрее, чем оригинального. Затем происходит
постепенный возврат к оригинальному графу. При этом может быть
использован уточняющий алгоритм, например, алгоритм KL/FM.
Многоуровневый метод RSB (MRSB) преобразует исходный граф,
используя понятие максимального независимого множества графа и
алгоритм RSB для разбиения графа. Известно несколько похожих
методов, которые используют понятие максимального паросочетания
графа на этапе его преобразования. Максимальное паросочетание может
быть найдено с помощью простого жадного алгоритма.
При многофазной стратегии балансировки нагрузки на каждой фазе
применяется метод многоуровневой балансировки на основе алгоритма [6].
Результаты предыдущей фазы учитываются при переходе на новую фазу.
С каждой новой фазой качество разбиения графа и балансировки нагрузки
улучшается.
В работе [7] предложен генетический алгоритм многоуровневого
разбиения графа. Хотя данный алгоритм формирует высококачественное
решение задачи, чрезвычайно большое время его работы не дает
возможности применить этот алгоритм в типичных задачах. Авторы
работы [7] предлагают использовать генетический алгоритм при
формировании тестов (benchmarks) для алгоритмов разбиения графов.
Стандартный подход к задаче разбиения графов имеет серьезные
недостатки. Задача разбиения графов не вполне адекватна задаче
балансировки нагрузки. Величина потока сообщений, передаваемых между
процессорами, в действительности не пропорциональна числу разрезанных
ребер графа и слабо предсказуема коммуникационными затратами [8].
Основы классификации методов балансировки нагрузки, которые
можно применять при распределенном моделировании цифровых
устройств, показаны в таблице 1.
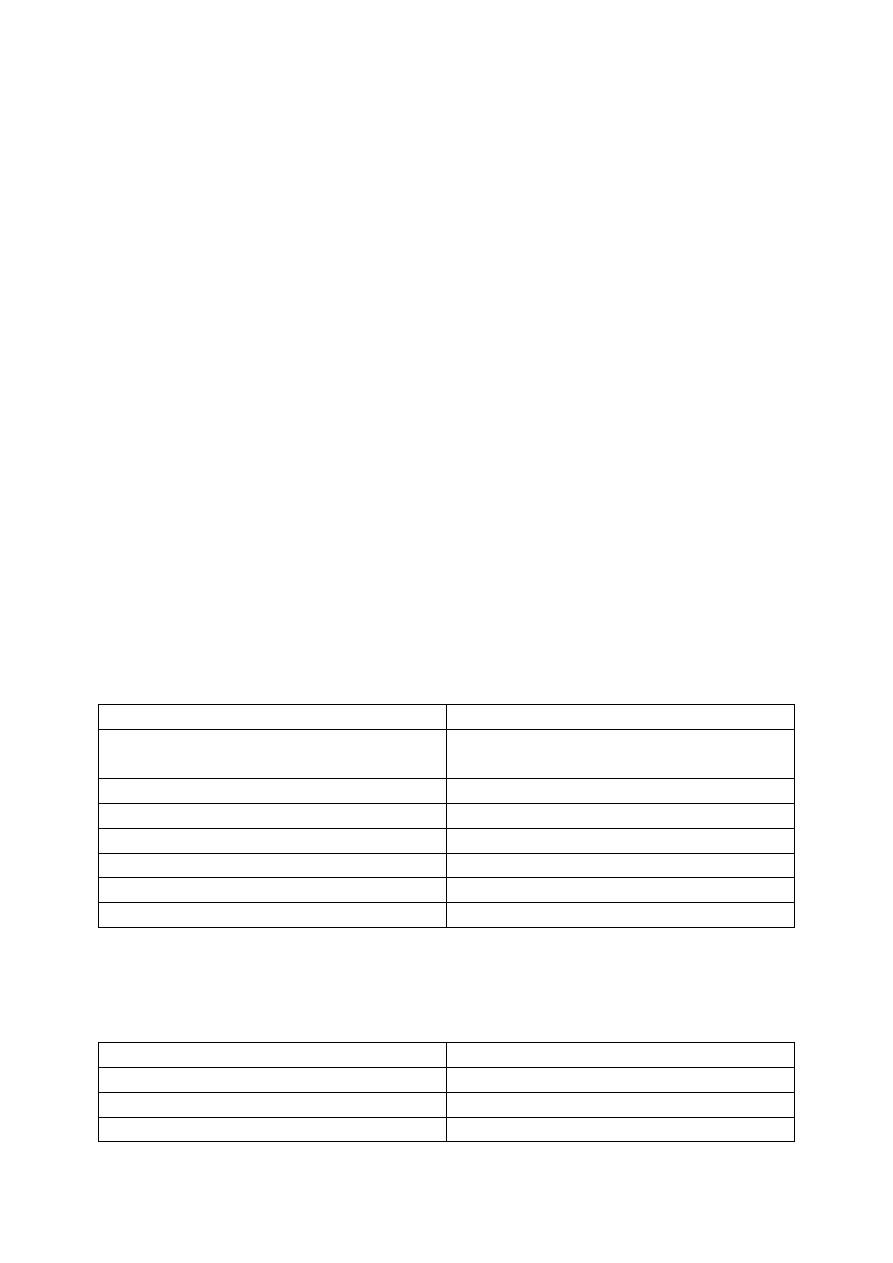
Таблица 1. – Классификация методов балансировки
Геометрические
Структурные
Алгоритм RCB
Рекурсивная структурно-уровневая
бисекция
Алгоритм RIB
Жадные алгоритмы
Алгоритм URB
Алгоритм RSB
Локальные
Уточняющие
Алгоритм Кубенко
Алгоритм KL
Алгоритм Ху и Блейка
Алгоритм KL/FM
Алгоритмы, управляемые запросами Алгоритм имитации отжига
Таблица 1. – Классификация методов балансировки (окончание)
Многоуровневые Master/Slave
Алгоритм MRSB
Алгоритм Фрамонто
Алгоритм Кариписа и Кумера
Алгоритм Херинга
Алгоритм Вальшава
Алгоритм инициативного сервера

Заключение
Большинство пакетов балансировки нагрузки предназначено для
решения
статической
задачи
балансировки.
Среди
алгоритмов
динамической
балансировки
нагрузки
большинство
является
последовательными. По
скорости и качеству, лучшим среди
последовательных алгоритмов балансировки является многоуровневый
метод Кариписа и Кумера, который использует быстрый жадный алгоритм
на этапе разбиения графа и алгоритм KL/FM на этапе уточнения.
Перспективным
направлением
исследований
в
области
распределенного моделирования цифровых устройств является разработка
эффективных параллельных динамических алгоритмов балансировки
нагрузки процессоров.
Литература
1.
Отчет по научно-исследовательской работе Г23-2000 “Развитие
теории распределенных вычислений в специализированных сетях
для автоматизированного проектирования ЦУ в базисе ПЛИС”.
Донецк: ДонНТУ, 2001. – 280 с.
2.
Hendricson B., Devine K. Dynamic load balancing in computational
mechanics. //www.cs.sandia.gov/~bahendr/load balancing
3.
Hering K., Loser J., Markwardt J. dlbSIM – a parallel functional logic
simulator allowing dynamic load balancing. //Proc. of DATE’01.IEEE
Press. 2001.- P. 471-478.
4.
Асад
Ахмад.
Динамическое
выравнивание
нагрузки
в
распределенных
вычислительных
системах.
Автореферат
диссертации. К.: 1996.- 22 с.
5.
Chamberlain B.L. Graph partitioning algorithms for distributing
workloads of parallel computations.//www.cs.sandia.gov/~cham/balance
6.
Walshaw C., Cross M. Mesh partitioning: a multilevel balancing and
refinement algorithm. //SIAM journal science computing
.
–2000. - № 1. -
P. 63-80.
7.
Soper A.J., Walshaw C., Cross M. A combined evolutionary search and
multilevel optimization approach to graph-partitioning. //Journal of global
optimization.–2004.- № 1. - P. 225-241.
8.
Hendrickson B. Load balancing fictions, falsehoods and fallacies.
//www.cs.sandia.gov/~bahendr/load balancing/fictions






